Updated 6/15/2022
“An investment in knowledge pays the best interest.”
As investors learn more about our investments, we become better investors. One of the many things I enjoy about investing remains the continual learning and the bottomless subjects to learn.
In that vein, learning to value a bond is high on my list of subjects.
Similar to valuing stocks, bonds offer the same valuation challenges, but the subject does not get covered much unless you study for the CFA certification. Or if you are a serious bond investor.
Luckily, the method we will discuss today is straightforward to learn and implement.
Investing in bonds is a subject that confounds many individual investors, and I hope our discussion today helps clear up any confusion.
In today’s post, we will learn:
- Bond Basics Overview
- How Do You Calculate the Value of a Bond?
- Bond Valuation Examples
- Bond Valuation FAQ
Ok, let’s dive in and learn more about bond valuation and how to put it into practice.
Bond Basics Overview
Valuing a bond is a technique that determines the fair value of a particular bond.
Many characteristics of valuing a stock are present when valuing a bond, including computing the present value of a bond’s future coupon payments.
Most investors would relate to cash flow, which equals the coupon payments of a bond for valuation. Another aspect of valuing a bond remains to determine the bond’s face value or the par value.
Bond par values and coupons remain fixed upon sale and use bond valuation to determine the return rate required to ensure a bond investment is worthwhile.
Before we tackle valuing a bond, let’s look at a quick overview of corporate bonds.
Corporate bonds are bonds issued by different corporations to fund various projects. All corporations can issue bonds, for example, Microsoft, Ford, and Walmart.
Corporate bonds generally offer higher yields than Treasury bonds because corporate bonds offer a greater risk of default than their treasury cousins. All of which makes the corporate bonds riskier, and many different types of corporate bonds concern levels of risk and yields.
Bond yields closely align with corporate bonds’ ratings or riskiness. Typically, the higher the risk, similarly, the higher the yield. We base the bond valuations on the same financials we use to value the stock. Microsoft’s bond remains the same as the stock equity for Microsoft; they base Microsoft’s ratings on the same basis.
The valuation of a bond is similar to that of stock, depending on the present value of upcoming cash flows, discounted at an appropriate risk-adjusted rate, which remains similar to a discounted cash flow that we use for valuing Microsoft.
Let’s talk about yield a bit. The yield for a bond equals the total return you receive for investing in that bond. The yield tells an investor how much they will receive for that investment.
Another aspect of analyzing bonds equals the yield to maturity, which we quote as the bond equivalent yield. The yield to maturity makes bonds easier to compare, as they examine the period closer to the bond’s maturity.
For example, Treasury bonds yields tie to the Fed’s Fund rate, an interest rate risk premium, and an inflation risk premium. Corporate bond investors demand a higher yield because of the risk of default.
The tying of the return is close to that yield. For example, the risk of defaulting on a company’s bond, such as JC Penney’s, is far greater than Microsoft. And for that reason, the yield or coupon of JC Penney’s is far higher than Microsoft’s, as the only reason anyone would take on that risk of default from JC Penney’s is to earn more money.
Understanding a bond’s yield is important to valuation as the return we expect from our investments centers around those yields or returns.
Related to those yields are the discount rates or required rates of returns we expect for our investments.
The same rates we use for a company’s equity are the rates we use to evaluate its debt or bonds.
Therefore, if you understand how to calculate a discounted cash flow, you can easily calculate a bond’s value.
Let’s move on and discuss next exactly how to value a bond.
How Do You Calculate the Value of a Bond
As we value a bond, several factors are the annual or semi-annual coupon payments and the bond’s face value.
The formula adds the present value of the expected cash flows to the bond’s face value’s present value. Below is the following formula for our valuation.
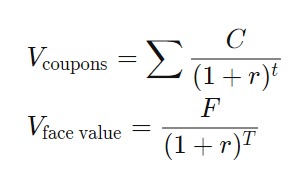
Don’t worry; we will help you decipher all the above Greek!
Relating to the symbols from above:
- C = future cash flows or coupon payments
- r = discount rate or yield to maturity
- F = face value of the bond
- t = number of periods or years
- T = time to maturity
Let’s use an example to lay out the best way to work through the above formula.
For example, let’s find a corporate bond value with an annual interest rate of 5%, making semi-annual payments. After two years, the bond matures and repays the principal. For our purposes, let’s assume a yield to maturity of 3%.
Face value of the corporate bond = $1000
Annual coupon rate = 5%, therefore, semi-annual coupon rate = 5%/2 = 2.5%
To find the coupon payment per period:
C = 2.5% x $1000 = $25 per semi-annual payments
To find the total number of periods we receive coupons, we take:
t = two years to maturity x 2 payments per period = 4 total periods or total coupon payments received
T = 4 periods
Now we can determine the present value of those coupon payments by looking at the following:
Present value = C / (1+YTM) raised to the period in question.
Now substituting the information, we have gathered:
Semi-annual coupons – $25
Yield to maturity – 3%
Total periods – 4
Present value of coupon payments = 25/(1.03)^1 + 25/(1.03)^2 + 25/(1.03)^3 + 25/(1.03)^4
Present value of coupon payments = 24.27 + 23.56 + 22.88 + 22.21
Present value of coupon payments = $92.93
We can now calculate the present value of the bond’s face value when the bond matures at the end of the fourth period. Please think of this as the present value of the bond’s terminal value because, in reality, the bond has come to the end of its life as it matures and the principal is due.
We use the same formula to find the present value of the cash flows of the coupons.
Present value of the face value = 1000 / (1.03)^4
Present value of the face value = $888.49
To find the bond’s present value, we add the present value of the coupon payments and the present value of the bond’s face value.
Value of bond = present value of coupon payments + present value of face value
Value of bond = $92.93 + $888.49
Value of bond = $981.42
A natural question one would ask is, what does this tell me?
When investing, we always hunt for value, whether socks or stocks. We all want to buy something for less than it is worth and sell it for more than it is worth.
Or buy low and sell high, the maxim of every investor.
To put the above perspective into context, think about if you had purchased the bond at a par value of $1000 today, then the value you receive when the bond matures is less than the money you paid.
No one wants that scenario. Instead, you would try to find the same bond for less than the present value. Remember that bonds trade on markets the same as stocks, albeit at much higher levels as most bonds trade in groupings of $10,000 to $100,000 lots.
Rather you would be better served to find a bond that is trading below our present value calculations.
For example, let us assume all things are equal, with the same par value, discount rate, and years to maturity. But if the yield to maturity is different from our 3%.
Look at the following numbers:
- 1.5% – $1,000
- 2% – $980.96
- 2.5% – $962.38
- 3% – $944.24
- 3.5% – $926.54
Based on the above numbers, which would you rather own, the bond with a present value of $981.42 or the bond with the present value of $944.24?
All things being equal, we would want to own the bond with a higher yield to maturity.
The above illustration clearly outlines one of the advantages of investing in a higher-yielding bond. But one item this all doesn’t consider is the risk involved with the higher-yielding bond.
The bond rating agencies, Moody’s, S&P Global, and Fitch, are the acknowledged experts in debt and set the ratings that govern bonds.
Generally, the lower the rating of a bond, the higher the yield; likewise, the higher the rating, the lower the yield.
Thus, the lower-rated bonds carry higher yields. But they also carry a higher risk of default. And that means more opportunity cost means you will lose your investment.
Remember that typically, higher yields equate to more risk of default.
We can look up the bond rating of any company that issues debt by looking at any rating agency site. I personally use Moody’s, and they offer some great commentary on debt and credit that are extremely insightful.
Ok, let’s next take a look at some real-world examples.
Bond Valuation Examples
I want to look at the first example from the tech world, AMD, the semiconductor chip producer.
The company currently carries a credit rating from Moody’s of Baa3, considered investment grade, but at the bottom rung of that scale.
Some stats for our calculations:
- Coupon rate – 7.5%
- Par value – $1,000
- Years to maturity – 2
- Coupon paid – Semi-annual
Now, let’s calculate what we base our bond’s present value on the above numbers.
Value of coupon payments = $1,000 x 7.5% = $75
The total number of payments over the two years equals two years; two payments a year give us four total payments.
Based on the discount rate for AMD’s equity, the discount rate for the bond is 7%, which we will assign to all of the following calculations to remain consistent.
If we input the numbers into the formula, we come up with a present value of:
Present value of coupons = 75/(1.07)^1 + 75/(1.07)^2 + 75/(1.07)^3 + 75/(1.07)^4 = $137.74
Now, for the present value of the face value of the bond.
Present face value of the bond = 1000/(1.07)^4 = $748.62
Present value of AMD’s bond = $137.74 + 748.62 = $886.36
Let’s look at another bond in the same industry, Qualcomm. The company currently carries a bond rating of A- from Moody’s, considered investment grade.
The coupon rate is set at 3%, and the bond is sold at a par value of $1000 with a maturity of two years.
So looking at the same rates as AMD for the discount rate, which is 7%.
Because the coupon is 3%, our annual coupon payment is $30, and then our semi-annual payment is $15.
Now, find the present value of those semi-annual payments, four total payments.
Present value of coupons = 15/(1.07)^1 + 15/(1.07)^2 + 15/(1.07)^3 + 15/(1.07)^4 = $55.10
Present face value of bond = 1000/(1.07)^4 = $748.62
Present value of bond = $55.10 + $748.62 = $803.72
Now, if we compare our two bond present value calculations:
- AMD – $886.36
- Qualcomm – $803.72
We can see the bond for AMD holds more value if we were to buy the bond today, which supports the fact the coupon payments you receive from the bond remain worth more.
Which is the payment we get for investing in a riskier bond like AMD. And is not an indictment on AMD but rather a comment on the impact credit ratings have on bonds and investing in those bonds.
Let’s say, for giggles, we bought the same Qualcomm issue when it was issued ten years ago. Using the same discount rate, we find:
- Coupons – $257.53
- Face value – $776.84
- Total present value – $1034.37
I would like you to notice the present value of the bond’s face value, which is $776.84. A couple of ideas to remember, when you purchase your bond for $1000, you will receive the initial $1000 back, but the additional $257.73 in coupon payments you will receive over the ten years you own the bond.
As the bond approaches maturity, it gets closer to that original face value you paid. When you invest in a bond, you pay for the coupon payments, plus any appreciation or depreciation.
Here are a few resources to help with these calculations, in case the math is not your cup of tea.
Bond Valuation FAQ
Below are the answers to some common bond valuation questions.
- What is the bond valuation formula?
The bond valuation formula is as follows:
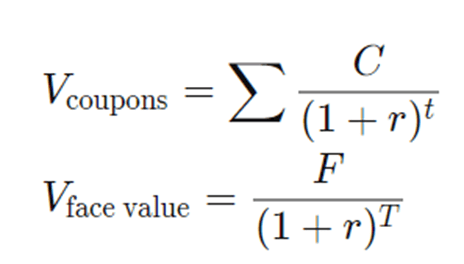
Relating to the symbols from above:
- C = future cash flows or coupon payments
- r = discount rate or yield to maturity
- F = face value of the bond
- t = number of periods or years
- T = time to maturity
- What are the steps of bond valuation?
We can price a bond using a four-step process while plugging in a few numbers.
- Calculate the face value, annual coupon, and maturity date.
- Calculate the expected cash flows for the bond’s coupon.
- Discount the bond’s coupon cash flows to the present.
- Value each cash flow for the bond.
The steps remain similar to valuing the same company with a discounted cash flow model; only we use the cash flows generated by the bond’s coupon and the bond’s face value. These both comprise the return we get from our bond investment.
- What are the three ways to value a bond?
The three methods include the above steps; we value the bond’s face value, the cash flows generated from the annual coupon, and the time value of money based on the bond’s maturity date.
Final Thoughts
At the end of 2021, the size of the US bond market had reached $46 trillion. With the size of the bond market dwarfing the equity markets, we should strive to understand bonds and how to invest with them.
The bond valuation method we used today continues as a useful exercise to find those bonds’ value. And it remains a good idea to look at the credit quality of any company you want to buy and understand what kind of debt they offer and when it matures.
Debt is one of the triggers of bankruptcies, so understanding how to analyze credit, at least on a superficial level, is helpful.
Investing in bonds or bond funds remains a great way to diversify your investments, and I have discovered that the more we know, the more comfortable we are with investing in an asset class like bonds.
With that, we will wrap up our conversation on bond valuation.
As always, thank you for taking the time to read this post, and I hope you find something of value on your investing journey.
If I can be of any further assistance, please don’t hesitate to reach out.
Until next time, take care and be safe out there,
Dave
Dave Ahern
Dave, a self-taught investor, empowers investors to start investing by demystifying the stock market.
