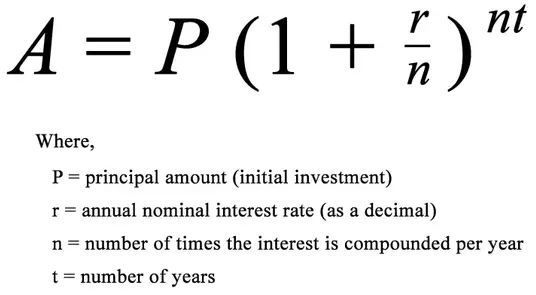Ever wanted to illustrate exactly how powerful compound interest can be? Wanted to have an Excel function to do it for you? This post reveals the continuous compound interest formula and how a function built into Excel will calculate it for you.
Click to jump to a section:
- Why is Compounding Important?
- Apply Compound Interest to Your Emergency Fund
- The Math Behind Compound Interest
Why is Compounding Important?
“Compound Interest is the eighth wonder of the world. He who understands it earns it…he who doesn’t, pays it”
– Albert Einstein
This is truly one of my favorite quotes ever. At first, I really didn’t understand it. “Yeah, you earn interest on your money…. who cares? That happens in a bank account too.” Boy, was I wrong.
This quote is truly what inspired me to start investing in the stock market. The concept of compound interest is pretty simple, really. Compounding is earning interest on your principal investment and all previously-earned interest. Think of it as earning money on your earned money.
For example, if you earn 6% on $1,000, you will then have $1,060. But, the next time you earn 6% interest, it will now be on $1060 instead of $1,000, which will result in a new value of $1,123.60.
Not a huge difference for this time, but it was $3.60 more than that $60 that your 6% interest on $1,000 generated. To explain this a bit better, I’ll put it into a real-life scenario I went through with my wife less than a week ago…
Apply Compound Interest to Your Emergency Fund
We’ve finally reached the point where we have a sufficient emergency fund. So now the thought process is, what do we do with it?
Previously, it had just been sitting in my bank account, earning a whopping .01% interest. Yes, I said .01%.
I was shocked when I saw it at first, but I started doing more research and realized it was pretty common, unfortunately.
I then started looking into some high-yield savings accounts, and from hearing some recommendations of Ally from Andrew on the podcast, I decided that I thought that was the best way to go about holding our emergency fund.
Now, my wife is typically very conservative when it comes to money, as am I, but she gets skeptical of doing things that might seem out of the ordinary. Such as investing in an online-only bank like Ally or Sofi, but I convinced her to do it by showing her some Cold. Hard. Facts.
The truth is, if you’re holding onto cash in a normal bank account and not putting it in a high-yield bank, you’re volunteering to lose money. Returns on high-yield savings accounts are guaranteed. As long as you’re FDIC insured, the risk is 0.
So, the question is, how did I convince her?
The Math Behind Compound Interest
It was easy, really – I showed her the value of the compound interest. But to share the results without first understanding the math is like giving a man a fish instead of teaching him how to fish! So, here we go – welcome to the Continuous Compound Interest Formula:
This formula might seem like a bunch of nonsense, but all you really need to know is:
- Your starting investment
- The rate of return
- Amount of years it will grow
- The frequency of the compounding each year.
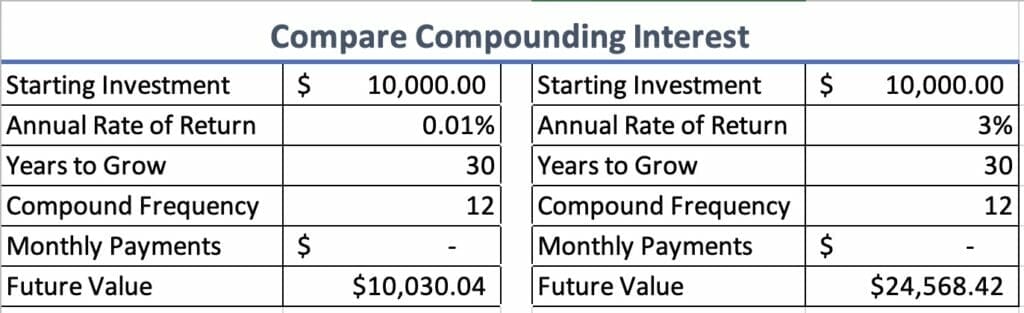
For instance, below is the situation that I explained to my wife. If we took $10,000 and kept it in our current bank account, earning .01% interest, for 30 years, compounded monthly, we would earn $30.04 on our investment.
BUT! If we put it in the Ally account, we would have earned $14,568.42 over our initial $10,000. I know that a little more than doubling your money in 30 years isn’t exactly a staggering outcome, but that’s not the point. The point is that by having that money compounding month after month on itself, we realize much greater returns than if we hadn’t allowed it to do so.
Excel has an awesome function that allows you to do this independently. And it’s rather simple – you don’t have to be a numbers nerd (like me) to run some situations! Look out below!
=FV(rate, nper, pmt, [pv], [type])
Simple, right? Let me explain:
- FV = Future Value
- Rate = Interest rate per period of compounding
- NPER = total number of payment periods
- PMT = The payment made each period
- PV = this is optional – but it is the present value of future payments.
- Type = this is also optional. If you select 0, it’s that the payments are at the beginning of the period; 1 is that they’re at the end. If you leave it blank, it’s 0.
So, let’s look at the picture below:
- FV = B5
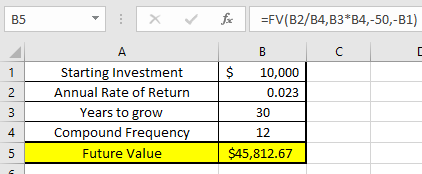
- Rate = B2/B4. What this is doing is I’m putting the APR in cell B2 and then the compound frequency (once/month) to get a monthly interest rate. (.023/12).
- NPER = B3*B4. This then gives me the total number of payment periods (12 months * 30 Years).
- PMT = 0. I’m not adding any additional money each period.
- PV = -B1. This is just stating the investment of $10,000.
- Type = left blank. It will compound at the start of each month.
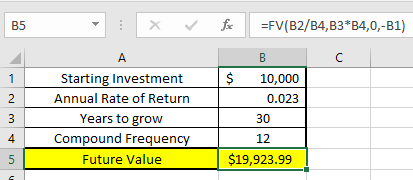
This might still seem confusing, but I guarantee that if you put this in excel in the format I’ve laid out, you will be able to walk through it step by step and get yourself a number. “What if I want to contribute money each month to this?” Say, like $50/month…EASY! All you need to do is change the PMT to a negative contribution. For instance, I’m putting -50 to show a contribution of $50/month in the below example.
You might be wondering why these numbers are negative, but it’s because this function is used as a payoff calculator rather than building interest, but they’re the inverse of each other, so they work the same.
Now, I will admit these are somewhat boring examples, but let’s take a look at if we did this in the stock market!
I have two examples below.
Both include making monthly contributions of $150, but one is if we realized an annual return of 6%, which is what I like to use as a conservative estimate when planning my future, and the other is looking at a 20-year average S&P 500 return of 9.95%, shown below:
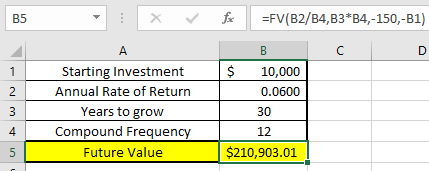
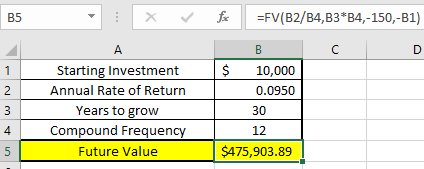
The importance of this article is to get you excited about compound interest and to teach you the ability to understand the continuous compound interest formula.
The formula truly is fairly simple to understand, and in my case, once I got it, I GOT IT. Like it just suddenly clicked.
This same concept can be used for DRIP, which Andrew has talked about many times. If you know your initial investment, interest rate, time frame, compounding frequency, and contributions, then you are so close to understanding where you can be and helping you further prepare for your financial future… All it takes is a little bit of comprehension and willingness to open up that Excel spreadsheet!
