If you’ve ever listened to even 5 minutes of a Financial Independence podcast, then you’ve likely heard something about the 4% rule.  The 4% rule is a very simple rule of thumb, but for someone like myself that loves to dive into the numbers – I always asked myself, actually how long will my money last?

If you haven’t heard of the 4% rule, let me give you a quick summary – essentially it’s a rule that says if you invest your money into a pretty conservative mix of bonds and stocks and you withdraw 4% every year then you will never run out of money.

Sounds pretty legit, right?  So, in other words, if you had $1,000,000 saved up/invested then you could essentially withdraw 4% of that, or $40,000, every single year and never run out of money!  So, the question is – does it actually work?

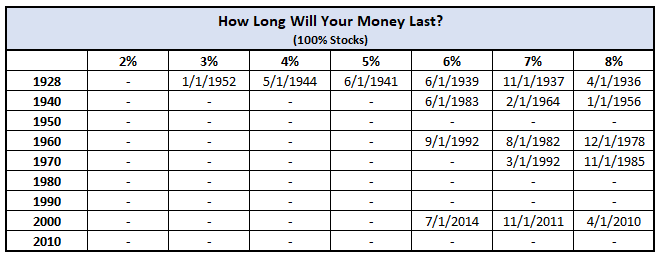
Well, I first wanted to test this out by doing a portfolio that was 100% invested in the S&P 500.  I went back and got the earliest data that I could, which was 1/1/1928, and then pretended that I invested $1,000,000 into the stock market at that time.  Every single month I would take out .33% (4% annually/12 months = .33% each month) of $1,000,000, or $3,333 because that’s 1/12 of 4% of my initial investment of $1,000,000. 

After taking that amount out, the rest would be invested for a month where I would then take out another $3,300.  After repeating this process month after month, the results were in…I would run out of money… on 5/1/1952!  So, my money only lasted 24 is years being invested 100% in stocks. 

I wanted to dive a little bit deeper into this to see how things would’ve shaped out with this 100% stock scenario by investing my $1 million in 1928, and then every ten years from 1940 – 2010.  I also wanted to see how things would change if I changed the amount that I took out each year, so I ran a range of annual distributions from 2-8%. 

What do you think would happen? 

The results are pretty stunning!

If I started in 1928, I would’ve run out pretty early as I already mentioned.  But any other 10-year period I would’ve made it all the way through until today even at a 5% withdrawal rate, so taking out $50,000 annually instead of the initial plan of $40,000.

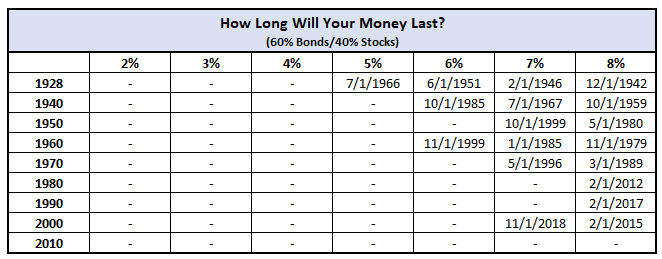
But, that’s not the essence of the 4% rule.  I ran another scenario where I would invest 60% in bonds and 40% in stocks and assumed that my bonds would grow 5% annually as the average since 1928 has been 4.88% per Mindfully Investing. 

When I did this, the new date that I would’ve run out of money is…. NEVER!  I’d still be sitting here right now with without running out of money.  And actually, my stockpile would’ve grown from $1 million to nearly $20 million!  Zoinks.  That’s pretty dang impressive.

Looking at the table below, you can see that this rule is really destined for success as long as you can make sure that you’re comfortable with the amount that you’re withdrawing at the beginning:

It immediately stands out to me that there is not a single time period where I’d run out of money until I get to 5%, and then each percentage incremental after that I gain more and more run out periods.  That’s not a coincidence.  When 60% of your portfolio is in bonds, you’re going to receive a much more conservative return than you would with stocks.  That means lower highs and higher lows – just much steadier and less volatile than the stock market.

When you’re not working and just banking on these distributions, then this is much rather preferred.

It’s important for me to note here as well that these investments don’t take into account any sort of dividend payments either, so you’d see an even longer period of being able to sustain this income and this should be digested as an ultra-conservative look.

My takeaway from this data is that the 4% rule absolutely can work as long as you can stick to the two following rules:

• You invest in a conservative mix of bonds and stocks similar to my 60/40 ratio
• You properly plan for your future and build enough of a buffer for withdrawals

The second rule is much harder to do and probably even more important.  If you plan to implement this rule with $1 million but you need $60,000 each year then you’re already pulling out 6% of your investment and guess what, with inflation you’re going to need even more money going forwards!

To figure out how much you need to save, you should simply take the amount that you need each year and then divide it by 4%.  So, for instance, if you need $50,000 each year, then take $50,000/.04 = $1,250,000. 

If you want to be even more conservative, then stick with the $50,000 and now divide it by 3% so you’ll now need $1,666,667 saved/invested to start your life of the 4% rule, although it would be really be the 3% rule in this case.

If you want to get even more conservative, bump up your $50,000 a bit to say, $65,000, and then divide it by 3%.  Your new total is $2,166,667. 

At the end of the day, the 4% rule is nothing but a rule of thumb.  It’s something that mathematically works but unfortunately things are never perfect in life.  You can always plan but sometimes unexpected things happen, and we can’t do anything about it.  All that we can do is when we’re planning our lives, we need to plan them in a way that’s much more conservative than what we think we will even need. 

Honestly, this is really a mindset more than anything else.

The more conservative that you are, the better chance you have of being prepared for your future life.  And I don’t mean in your investments, but in your life choices.  Don’t just get to the minimum range of the 4% rule and then call it quits. 

You need to prepare for the worst and hope for the best and while math shows that the 4% rule is something that has some legit validity to it, why not prepare for the worst and use a 3% rule for your own calculations.

So – how long will your money last?  Well, that’s really on you, young grasshopper – hopefully forever.