Both NOPLAT and ROIC can be easily misinterpreted and misused in its applications to understanding a business. NOPLAT gets especially mishandled due to its more well known cousin, NOPAT. Most of the time these are interchangeable, but when they’re not, it can really lead to a distortion in calculating ROIC.

What is NOPLAT?

NOPLAT stands for Net Operating Profit Less Adjusted Taxes, and is the numerator in the classic ROIC calculation.

As I discussed in the blog post about operating Invested Capital, operating ROIC, and how both of those calculations reflect different areas of business and management performance, NOPLAT also falls into the category of having the potential to be glossed over.

But it should not be, and let’s discuss why, with an example at the end where the difference between NOPLAT and NOPAT can lead to wildly variant ROIC results.

Back to the Basics: ROIC

But before even discussing NOPLAT vs NOPAT, we need to remind ourselves to the root of ROIC and why it matters.

ROIC, as we should know, stands for Return on Invested Capital, and helps investors understand how a business performs with an injection of capital. In general, a business with higher ROIC will need less capital to spurn growth and/or can achieve large growth rates with large reinvestments of free cash flow.

Not only does ROIC help measure a business’s efficiency and capital intensiveness, but it can also help analysts in estimating future growth.

By combining ROIC with a company’s retention rate, you can get a rough estimate of the company’s expected growth, leaving all other things equal. This is the simple formula for that:

Growth rate = Return on new invested capital x Investment rate

Example: Martin Marietta Materials ($MLM) retained about 55.3% of its free cash flow (measured roughly Cash from Operations – Capex). This was calculated by subtracting dividends paid and shares repurchased from this free cash flow estimate, and dividing it by FCF, to get a retained cash flow percentage estimate.

Taking this Investment rate and multiplying it by the company’s historical 5Y average ROIC on reinvested cash flows (from quickfs.net) of 7.7%, you get 4.26%, which could be used as a growth rate component from cash flows reinvested into a business, for valuation models such as a DCF.

While the likelihood of the company to continue to earn historical ROICs also needs consideration, just having this simple calculation can serve for a great reference point and is easy to internalize (I’ll show how operating ROIC would be a better proxy for this below).

Basically, we know how much the company likes to internally reinvest in itself. We know what they’ve been able to earn on (re)invested capital, and we can project growth from there.

NOPLAT vs NOPAT

NOPLAT is used to calculate (operating) ROIC because:

• Operating ROIC tries to separate the core business from all of the rest of the moving parts
• Taxes can be deferred or used as a benefit from year to year, distorting net earnings or cash flow
• Heavily leveraged companies can have large interest expense which weighs down earnings

The use of NOPLAT is not to say that earnings, taxes, or interest expense are not important. Instead, it’s meant as a tool for one specific purpose, to calculate the efficiency of the operating (or core) business.

After that, it’s up to the investor/ analyst to evaluate other components of the business and management with other special tools.

You’ll find that NOPAT (Net Operating Profit After Taxes) does all of the same things that the above bullets described about NOPLAT, at least most of the time:

• NOPAT = Focus on operating profit without taxes
  • Interest expense, depreciation, amortization not included yet
  • NOPAT = Operating Income x (1 – normalized tax rate)

Note: I sourced the formula from a great blog post with his contradicting points (with mine) about ROIC, for those of you interested in falling down the rabbit hole deeper.

The NOPLAT Formula

You’ll notice that the difference between NOPLAT and NOPAT is “Less Adjusted Taxes” versus “After Taxes”. I’ll leave it to the classic textbook by McKinsey & Company called Valuation: Measuring and Managing the Value of Companies, to explain the difference:

“For valuation and analytical purposes, income taxes need to be adjusted to a cash basis. Investors expect the company to continue to earn a return on the capital saved as a result of tax deferrals. Putting taxes on a cash basis is consistent with the treatment of deferred tax balances as capital on which investors expect to earn a return, just as they do on all other capital.”

McKinsey (in their 2000 version) recommended the following as one of the ways to calculate NOPLAT:

NOPLAT = EBITA – taxes on EBITA + changes in deferred taxes

Where,

taxes on EBITA =
Total income tax provision from income statement
+Tax shield on interest expense
-Tax on interest income
-Tax on non-operating income

Note: Keep in mind that this formula was published in 1999 before goodwill amortization over a straight line (like depreciation) was replaced by annual goodwill impairment tests. However, the general concept still seems to apply the same.

For the purposes of this article, and in the attempt to reconcile the FASB developments in the note above (regarding amortization), I will replace EBITA with EBIT.

So, we have the following as a formula:

NOPLAT = EBIT – taxes on EBITA + changes in deferred taxes

Where,

taxes on EBIT =
Total income tax provision
+Tax shield on interest expense
-Tax on interest income
-Tax on non-operating income

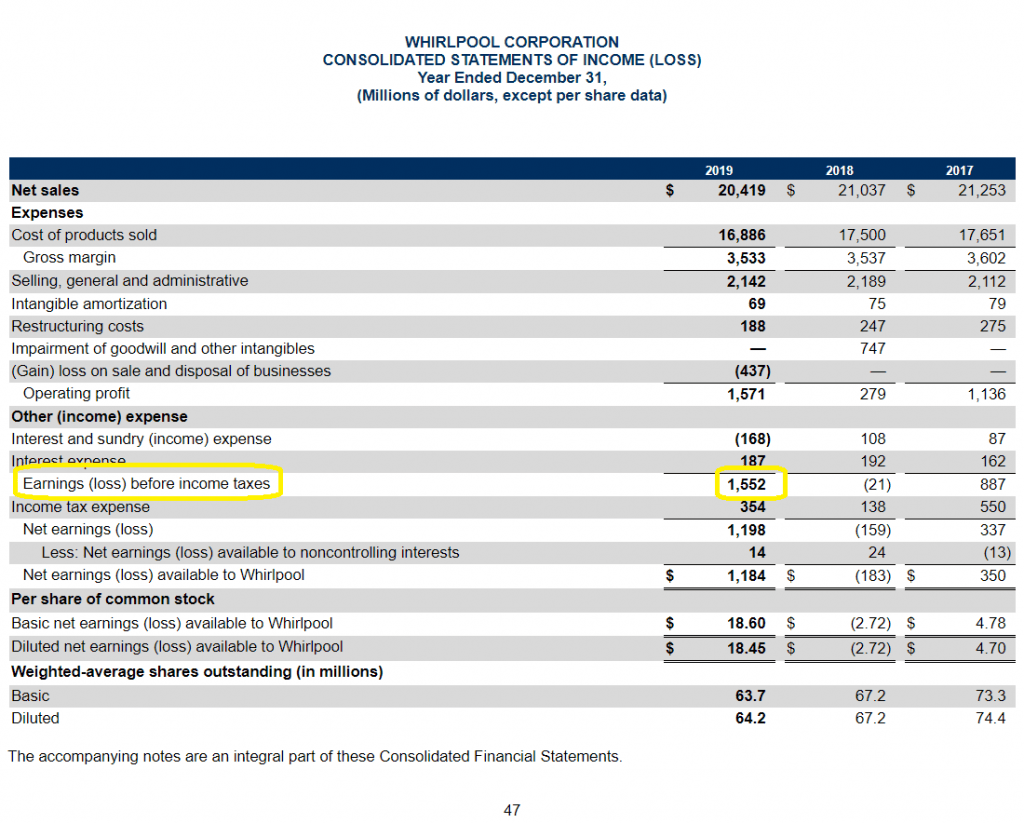
Taking this formula, I’ll illustrate an example calculation with a company called Whirlpool ($WHR).

EBIT can be sourced from the income statement, in this case = $1,552 million.

Total income tax provision = Income tax expense = $354 million.

Tax shield on interest expense is another fancy way of saying the tax deduction that the business will receive on the interest it must pay as it makes its debt payments. We can calculate this by taking Interest expense and multiplying it by the marginal tax rate (which we should find in the footnotes):

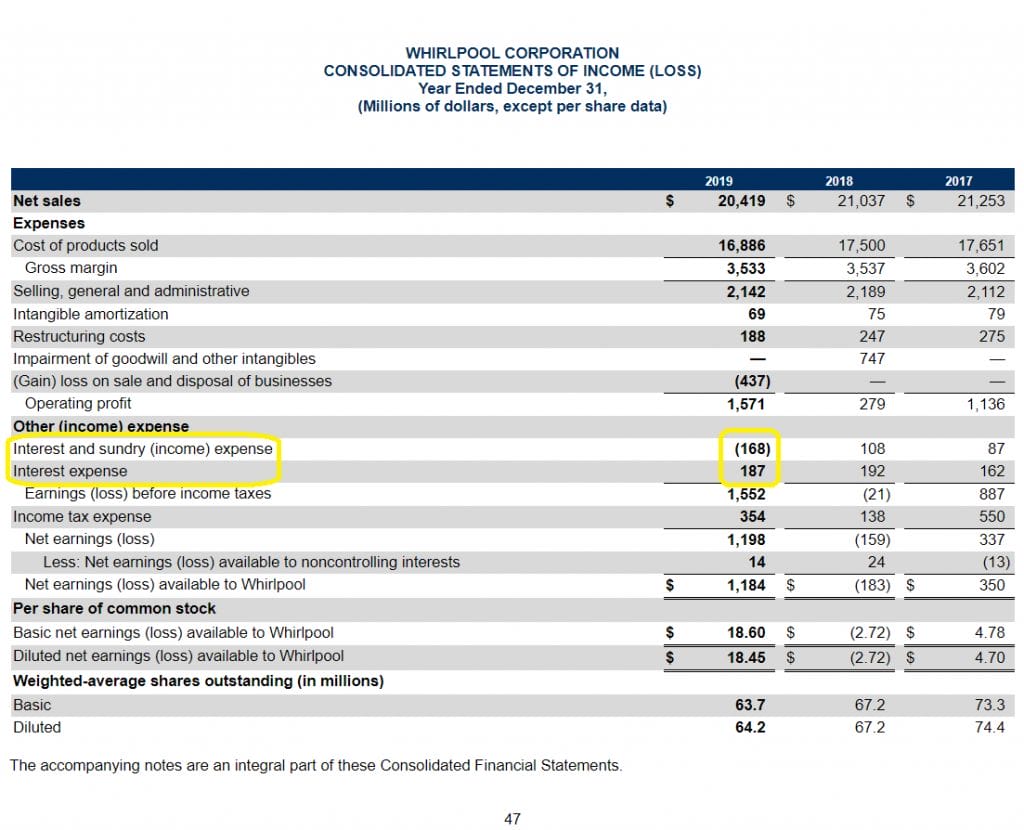
The net for interest expense in this case is $187 – $168 = $19 million.

Since the company anticipates a marginal tax rate of 20-25%, we’ll split the difference and use 22.5%.

Tax shield on interest expense
= Interest expense * marginal tax rate
= $19 million * (.225)
= $4.28 million

Tax on interest income doesn’t apply to $WHR, a business with no interest income for the year, so Tax on interest income = $0.

But, the tax on non-operating income can be found in the consolidated statements of comprehensive income, as an expense of $12 million.

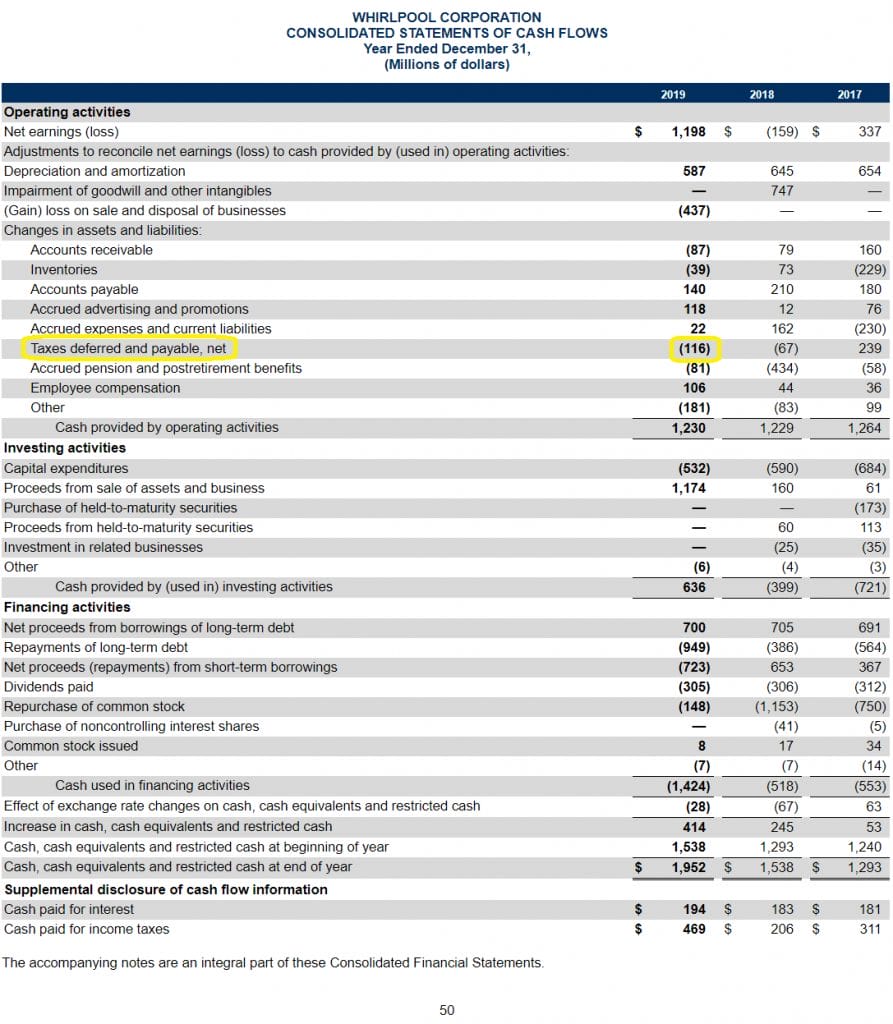
Finally, we can find the change in deferred taxes as a simple line item in the Cash Flow Statement = -$116 million.

Going back to the taxes on EBIT calculation:

Taxes on EBIT =
$354 million + $4.28 million – $12 million
= $346.28 million

Finally, putting all of the numbers together:

NOPLAT = EBIT – taxes on EBITA + changes in deferred taxes
NOPLAT= 1,552 – 346.28 – 116
NOPLAT = $1,089.72 million

Note that this is slightly lower than Net Income for the year ($1,198 million), which could mean that the company’s total business contributes more than the core business to earnings– but since it’s such a small difference, I’d say probably not.

When NOPAT Doesn’t Equal NOPLAT

Sometimes Adjusted Taxes aren’t the same as NOPAT. As explained above, when a company defers interest expense, it gets “taken” from interest expense but is paid with cash later when taxes are recorded in the income statement but added as a deferred tax liabilities on the balance sheet, which doesn’t take cash from operating cash flows.

To find a NOPLAT that is different from NOPAT, you have to look for deferred tax liabilities or assets, which is something I covered in-depth recently here.

Once you’ve determined your NOPLAT, you have the tools to calculate an operating ROIC, if you combine it with operating Invested Capital.

Operating ROIC can be very valuable in identifying businesses with great underlying core businesses but managements that are poor allocators (pushing down total ROIC), or vice versa.

In the case that management has been changed recently (as an example), this difference between using operating ROIC (and NOPLAT) vs firm-wide ROIC (and NOPAT) can be a potential hidden value unlock for the long term investor.