Have you ever tried planning for your financial future, only to realize how difficult it is to project into it? This post will cover how calculating the annualized rate of return can give a road map of what kind of future wealth to expect…
Click to jump to a section:
- Why Calculate it Yourself?
- Annualized Rate of Return Example
- Calculating the Formula with Excel
- Why Use This Formula
Question – what is the most desirable frequency for your interest to be compounded?
Answer: I’ll tell you later…
Why Calculate it Yourself?
If you have read any of my blog posts before, you probably will get the sense that I am a bit of a spreadsheet fanatic.
Rather than download Mint, I will create my own excel spreadsheet.
Rather than Google a compound interest or a loan payoff calculator, I will do it in Excel.
I prefer to do it this way. I think it helps me understand the numbers better and therefore helps allow me to make better decisions. It’s great to plug some numbers into a calculator that hand-feeds you a solution, but what do you really learn? By calculating it yourself, you can better grasp the importance of each variable.
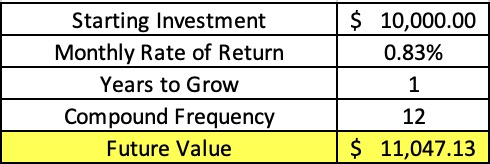
This post really goes hand in hand with my post about compound interest. If I invested $10,000 in a bank account that earned 10% interest, which was accrued at an annual rate, then I would have $11,000 at the end of the year, right? Right. BUT! My friends, what if it was compounded monthly? Well, then you would be in an even better situation! See below:
As you can see, if you compounded $10,000 at a monthly rate of .83% (10%/12 months) then you would have $11,047.13 at the end of the year rather than the $11,000 if it was compounded annually.
Long story short – the more frequent the compounding, the better. Future compounding can compound on previous returns, causing even more compounding in the future, and so on. The shorter the period between compounding, the more powerful.
Yes, I know this isn’t a compound interest blog, as I did that not too long ago, but I really wanted to set the stage to explain the annualized rate of return.
The annualized rate of return will take the rate of return you have realized so far and then expand it on an annual basis to give you the annualized rate of return.
Annualized Rate of Return Example
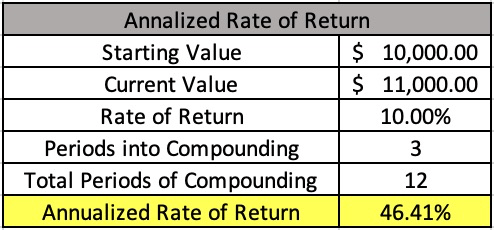
Let’s imagine that you invested $10,000 on January 1st, and on April 1st, that $10,000 investment had turned into $11,000. Simple math might make you think, “Well, I received a 10% return for ¼ of the year, so 10%*4 quarters = 40% annual return, or in this case, $14,000.” Simple enough, right? Well, I LOVE to tell you that you’re wrong – your annual rate of return is better.
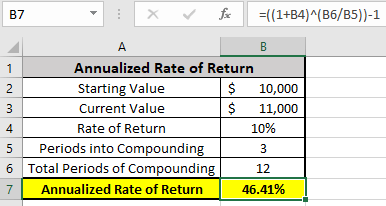
As you can see, your actual annualized rate of return is 46.41%. The reasoning for the increased return is simple: As your principal grows, the amount that generates interest also grows.
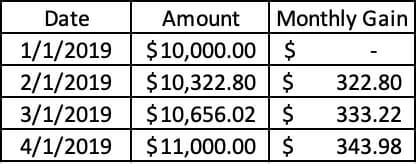
For example, if I earned 10% in a quarter, my average monthly interest rate isn’t 3.33%. It’s actually 3.228%. Make sense? It didn’t to me at first. Let me explain better below:
So, on 1/1, we started with our initial investment of $10,000.
By 2/1, that investment grew 3.228%, so my new balance was $10,322.80, or by $322.80.
By 3/1, my new balance had grown by 3.228%, but now I was earning 3.228% interest on $10,322.80 instead of $10,000. So my Monthly Gain had increased to $333.22 compared to $322.80 on 2/1.
Then by 4/1, the balance still grew by 3.228%, but the Monthly Gain was up to $343.98 since the interest was earned on $10,656.02 instead of $10,000.
I’m showing this compound interest math because it shows the root reason for calculating annualized returns.
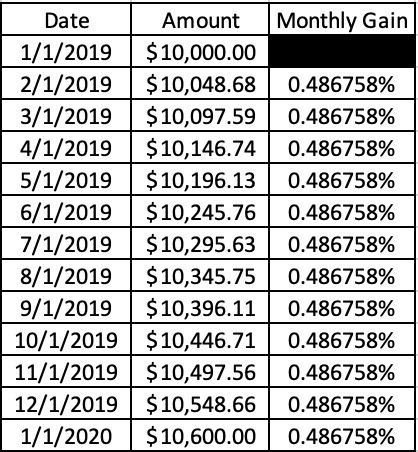
You have probably read in previous posts that I like to plan on a 6% annual rate of return as a safe, conservative estimate.
Achieving that 6% is not as simple as just assuming a .5% monthly return (6% annual return/12 months). If you do this, you’re not accounting for the compound interest component of investing. See below:
As you can see, a .486758% interest rate (or .49% if you’re not a fan of 6-digit decimals) will net you a 6% annual rate of return.
Hopefully you’re currently sitting there wondering how you can calculate your own annualized rate of return. Let me show you:
Calculating the Formula with Excel
Below I’ve included a screenshot of a previously used scenario where I had invested $10,000, and after three months, I had $11,000. I wanted to figure out if I maintained this same monthly rate of return, what would I have at the end of the year? To calculate this, you need 5 pieces of information:
- Starting Value (Cell B2)
- Current Value (Cell B3)
- Rate of Return (Cell B4)
- This is determined by taking B3/B2 – 1, or (11,000-10,000)-1
- Periods into Compounding (Cell B5)
- This is the amount of time periods that you are into the process. For example, if you’re three months into one year, it’s 3.
- Total Periods of Compounding (Cell B6)
- This is the total compound periods. So, one year is 12.
I have purposefully left the formula at the top of the screenshot, so you can see how to calculate this in excel.
- 1+B4
- This section is taking your interest rate (B4) + 1. You have to add one because since you’re gaining 10%, your new percentage is 110% (100% start + 10% gain) of your initial investment.
- B6/B5
- This is calculating the number of periods remaining
- – 1
- This is taking out the initial investment (100%) so you’re only capturing the incremental rate of return
The formula seems very complicated at first glance, but it really isn’t once you dig into it more.
Why Use This Formula
You quite possibly are sitting there thinking, “Ok, this is kind of cool, but I don’t see where I would ever really use this.”
I used to think the same.
But the more I got into investing, the more I wanted to learn. I love using this formula all the time to track how certain stocks have performed. I will frequently run hypothetical situations to evaluate how my investments would have done, and, in a sense, I post-audit myself.
I have frequently heard people say you should decide on your investments and move on, but I wholeheartedly disagree.
I think you can emotionally move on from that decision, but it’s important never to forget it.
Whether you made the right decision or the wrong one, there’s always a lesson learned. If you have flawed beliefs and continue just to make decisions and forget about them, will you ever really learn? I’m guessing not.
So…to answer my question from the beginning of this article…
What is the most desirable frequency for your interest to be compounded?
AS FREQUENTLY AS HUMANLY POSSIBLE
I’ll take my $10,000 investment and monthly compounding of .98% vs. your $10,000 annual compounding of 12% and we will see who comes out with a higher dollar value.
Spoiler: It’s me. By over $41.
